Well it’s good to see that you’ve decided to participate in Robotix 2016. Let’s get you through the event in a few easy steps through this easy to follow DIY.
The Sherlock robot is a basic differential drive chassis with a few sensors aboard. The two primary sensors are the HMC5883L magnetic digital compass that can be interfaced with the help of I2C communication protocol and the TSOP1738 IR receiver. Both of these are really common and the basic codes for both of them are pretty easy on a microcontroller like Arduino. Usage of these sensors is fairly simple and more information is available on our tutorial page for Sherlock. What matters most is the code and algorithms that drive your robot! That’s what this tutorial covers.
Round 1
The Round 1 can be completed without any significant algorithmic knowledge. The robot does not have to decode the entire map on the start node. On start node, the robot receives a message in the form:
400 12 51 72 500 400 22 51 2 260 20 500
The ‘400’ and ‘500’ are the start and end values of the message respectively. There are 2 pieces of information given by the message.
First:
- 12 denotes that it is the first of the 2 total messages.
- 51 is the ID of the start node.
- 72 is the finish point for the run. Let’s say the treasure is at node with ID 72. :-)
Second:
- 22 denotes that it is the second of the 2 total messages.
- 51 is the ID of the start node
- 2 is the ID of the next node connected to the start, at an absolute heading of 260 degrees wrt north. The cost to the path is 20. In Round 1, all the costs are set to 20 by default.
Thus now the robot has to align itself as close to 260 degrees wrt north as possible, and then move forward until it encounters node 2. When it reaches node 2, it receives a message in the form
400 11 2 5 120 20 500
11 denotes that it is the first of the total 1 message. 2 is the ID of the node, while the information is that the next node is node 5, at heading 120 degrees wrt north. So the robot now has to turn by 140 (260-120) degrees to align itself to that heading and move forward until it encounters node 5.
In a similar way, it has to keep moving and following nodes until it reaches the finish point, i.e. node 72.
Round 2
In Round 2, the problem becomes highly algorithmic and hence challenging. The start node now gives the robot an overview of the entire connected graph. The start node message thus now looks like:
400 13 51 2 3 4 450 3 2 5 450 4 2 5 6 450 5 3 4 7 450 6 4 7 450 7 5 6 8 450 8 7 9 72 450 500 400 23 51 72 500 400 33 51 2 220 20 500
Don’t be overawed by the length. The length would be much much more longer. And don’t be overawed by that too, everything would be handled by the microcontroller!
Here’s what every single word of that gibberish means:
As evident, there are now three pieces of information from this code, from the three pairs of start (400) and stop (500) bits. I’m going to cover the second and third parts first, as they are pretty similar to what was there in Round 1.
Second:
- 23 denotes that it is the second of the 3 total messages.
- 51 is the ID of the start node.
- 72 is the finish point for the run. Let’s say the treasure is at node with ID 72. :-)
Third:
- 33 denotes that it is the third of the 3 total messages
- 51 is the ID of the start node
- 2 is the ID of the next node connected to the start, at an absolute heading of 220 degrees wrt north. The cost to the path is 20.
Now coming back to the first information. The long message is decoded as follows:
- 13 denotes that it is the first of the 3 total messages
- 51 is the ID of the start node
-
After this the separator (450) separated numbers denote the nodes and their connections.
- So,
- 2 is connected to 3 and 4.
- 3 is connected to 2 and 5.
- 4 is connected to 2, 5 and 6.
- 5 is connected to 3, 4 and 7.
- 6 is connected to 4 and 7.
- 7 is connected to 5, 6 and 8.
- 8 is connected to 7, 9 and 72.
Hence the robot now knows a complete connected graph. Here’s roughly what it looks like:
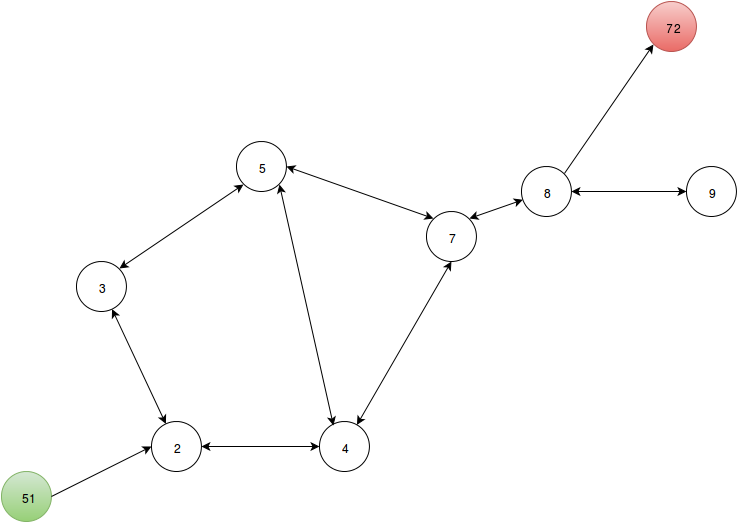
Thus now the robot has to align itself as close to 220 degrees wrt north as possible, and then move forward until it encounters node 2. When it reaches node 2, it receives a message in the form
400 11 2 3 150 10 450 4 100 15 500
Which means that the node 2 is connected to 3 and 4 at headings of 150 degrees and 100 degrees and via paths of costs of 10 and 15 respectively.
What remains unknown are the path weights to the end point. As the problem statement says, the robot has to minimize a weighted sum of path costs and no. of nodes. The no. of nodes problem is a simple one, akin to a shortest path problem in graph theory. It can be solved using a really simple technique called breadth first search (BFS)
Breadth First Search (BFS) Algorithm
Breadth First Search is an algorithm used for searching and traversing graphs. It is a really simple to implement technique to find the shortest way from start to end in a connected graph. In BFS, we keep marking nodes as visited as soon as we find a way to reach them, initially all being unmarked. Then we keep count of the minimum number of steps required to reach the node. We continue exploring neighbours of the visited nodes. Hence we are able to calculate the shortest path to reach the final node. When all the nodes are visited at least once, the algorithm stops and we get an answer, which can be proven to be right by the techniques of mathematical induction. Here’s a pseudocode that implements such an algorithm:
start at the source node S
put this in current level bucket
while we have not ran out of graph (next level bucket is not empty) and not found our target node
take a node from current level bucket – call it C
for each node reachable from current node C – call it N
(we can also check to see if it is visited node and skip it to avoid the cycles)
mark the predecessor of N as C
Check if N is our target node (that is have we reached the target node)
If YES, then exit
put this N in next level bucket
mark next level bucket as current levelAs you can appreciate, we can write a simple code to traverse such a graph. The information stored in Sherlock would mostly be in the form of an adjacency list, and BFS can be modified slightly to give our results in a O(nlog(n)) time complexity.
Another algorithm used to search graphs is depth first search (DFS), but it is not used to calculate shortest paths as the result may or may not be correct. Speed depends on type and shape of graph. If the graph bifurcates too many times, BFS may be quite slow, and DFS may cruise through to the end point. DFS is suitable to be used if the robot actually has to move to the end vertex without knowing the graph. Since all the motion to the end is happening in the code itself, we’d prefer an algorithm that gives us the correct answer.
The next problem lies with the path weights/costs. Minimizing costs on a known graph is an old and well solved problem, using a modified form of breadth first search algorithm, called Djikstra’s algorithm. Another algorithm A* (pronounced A-star) may be used too, but that’s just like the gamble between BFS and DFS. Djikstra’s algorithm always gives the correct answer, but might slow down a bit due to its nature of opening up all neighbours to a node in a highly divergent graph. Also the algorithm is valid only for positive edge weights, which is the case here. So we would not go into the Bellman Ford’s algorithm and stick to Djikstra and A*
Djikstra’s Algorithm
Djikstra’s algorithm, just like breadth first search traverses all neighbours of visited nodes and marks them visited, while keeping count of the minimum cost required to reach that node. It returns information for the minimum cost required to reach any node from the start point. It is simply a modification of BFS and hence the pseudocode is easy to understand.
Given a graph, G, with edges E of the form (v1, v2) and vertices V, and a
source vertex, s
dist : array of distances from the source to each vertex
prev : array of pointers to preceding vertices
i : loop index
F : list of finished vertices
U : list or heap unfinished vertices
/* Initialization: initialization every distance to INFINITY until we discover a path */
for i = 0 to |V| - 1
dist[i] = INFINITY
prev[i] = NULL
end
/* The distance from the source to the source is defined to be zero */
dist[s] = 0
/* This loop corresponds to sending out the explorers walking the paths, where
* the step of picking "the vertex, v, with the shortest path to s" corresponds
* to an explorer arriving at an unexplored vertex */
while(F is missing a vertex)
pick the vertex, v, in U with the shortest path to s
add v to F
for each edge of v, (v1, v2)
/* The next step is sometimes given the confusing name "relaxation" */
if(dist[v1] + length(v1, v2) < dist[v2])
dist[v2] = dist[v1] + length(v1, v2)
prev[v2] = v1
possibly update U, depending on implementation
end if
end for
end whileAs you can see, this pseudocode accounts for cyclic loops too, as it updates the node weights if it traversed the node again, and our event requires the same.
Here we attach a pseudocode for the A star algorithm, without explanation. Here’s the link.
So far so good. But as it may be evident, we have two main problems that YOU have to tackle to make a successful robot for event Sherlock.
- The Graph weights are not known at the beginning in round 2. You have to calculate the coefficients of the bi-quadratic weight functions, i.e. a,b,c,d,e as in the equation
a*x^4 + b*x^3 + c*x^2 + d*x + e - While doing so, it must not eat up the tiny memory of the Arduino!
Yes, the second problem is something you might not have thought of, and is a major one. One recommendation would be to use an Arduino Mega over an Uno, but a recursive code might even eat up a Mega’s memory. Well written iterative codes would work good both on Uno and Mega, with Mega having more margin for error. The Uno has 2 kilobytes of SRAM and the mega, 8 kilobytes. Considering 2 byte ints, it wouldn’t take too long to fill up, and recursive functions would fail almost definitely.
Another solution would be to use the Flash memory, the Uno has 32kb, while the Mega has a nice 256 kilobytes! The flash memory is best for data that is constant and does not need to be modified further. For example, our graph array or list can be safely stored in the flash memory without worries. For usage of the Flash memory on Arduino, check out this link.
The first part is where the essence of the event lies. The robot initially does not know anything about the edge costs. The robot initially would take a biquadratic equation and keep constructing simultaneous equations until they become 5 in number.
The five equations would be of the form:
x1 = 256*a + 64*b + 16*c + 4*d + e
x2 = 81*a + 27*b + 9*c + 3*d + e
x3 = 16*a + 8*b + 4*c + 2*d + e
x4 = a + b + c + d + e
x5 = eNow the robot would know the edge costs as well, and hence after that the robot will come to know the entire graph with the edge costs as well. Now after that it is simply a Djikstra’s algorithm problem which can be solved with ease. Using the iterative code, the robot can find the minimum cost path in seconds and then follow the headings to reach the end point.
So here’s to flaunt your algorithmic skills and be the eventual champion of Sherlock, Robotix 2016!