Introduction
A Rapidly-Exploring Random Tree is a randomised data structure that is designed for path planning problems.
Algorithm
In any image where RRT has to be implemented, there will be a start point, an end point and obstacles. The start point is taken as the first node, and the end point is taken as the last node. The first step is to generate a random node. Using distance formula, the node (in the tree) which has the minimum distance from this random node among all other nodes in the tree is identified. Starting from the nearest node, in the direction of the random node, a new node is generated at a predefined distance called step size. This new node is then added to the tree. These steps are repeated n number of times till the end point is added to the tree. Then a continuous path is traced from the start point to the end point which successfully avoids all obstacles. This process results into a tree-like structure, hence the name Rapidly-Exploring Random Tree.
The code explained
Let us take a sample image to implement the code on.
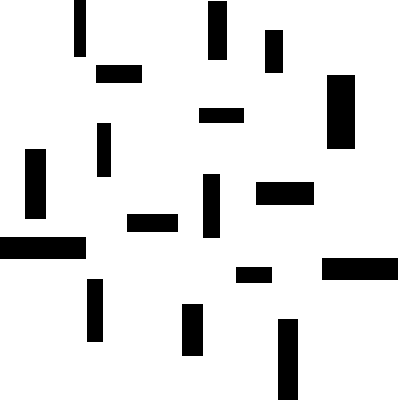
Following are some basic declarations:
typedef struct
{
int x;
int y;
}coordi;
struct Node
{
vector<Node *> children;
Node *parent;
coordi position;
}
Node start_node;
Node end_node;
Mat img;
Node* nodes[5000];
int totnodes = 0;
int reached = 0;
int step_size = 10;
int iter = 0;The init() function declares the position of the start point and the end point. The start point is marked blue and the end point red.
void init()
{
start_node.position.x = 50;
start_node.position.y = 50;
start_node.parent = NULL;
for(int i=start_node.position.x - 5; i <start_node.position.x + 5; i++)
{
for(int j=start_node.position.y - 5; j < start_node.position.y + 5; j++)
{
img.at<Vec3b>(i, j)[0] = 255;
img.at<Vec3b>(i, j)[1] = 0;
img.at<Vec3b>(i, j)[2] = 0;
}
}
nodes[totnodes++] = &start_node;
end_node.position.x = 350;
end_node.position.y = 350;
for(int i=end_node.position.x - 5; i < end_node.position.x + 5; i++)
{
for(int j=end_node.position.y - 5; j < end_node.position.y + 5; j++)
{
img.at<Vec3b>(i, j)[0] = 0;
img.at<Vec3b>(i, j)[1] = 0;
img.at<Vec3b>(i, j)[2] = 255;
}
}
srand(time(NULL));
}The near_node function is responsible for finding the nearest node in the tree for a particular random node (rnode). The node_dist function takes two coordinates as its input and returns the distance between them.
int near_node(Node rnode)
{
float min_dist = 999.0, dist= node_dist(start_node.position, rnode.position);
int lnode = 0, i = 0;
for(i=0; i < totnodes; i++)
{
dist = node_dist(nodes[i]->position, rnode.position);
if(dist < min_dist)
{
min_dist = dist;
lnode = i;
}
}
return lnode;
}The stepping function takes the random node generated (rnode) and its nearest node (nnode) in the tree as its input, and returns the coordinates of the step node. This function determines the step node by generating a new node at a distance of step_size from nnode towards rnode.
coordi stepping(coordi nnode, coordi rnode)
{
coordi interm, step;
float magn = 0.0, x = 0.0, y = 0.0;
interm.x = rnode.x - nnode.x;
interm.y = rnode.y - nnode.y;
magn = sqrt((interm.x)*(interm.x) + (interm.y)*(interm.y));
x = (float)(interm.x / magn);
y = (float)(interm.y / magn);
step.x = (int)(nnode.x + step_size*x);
step.y = (int)(nnode.y + step_size*y);
return step;
}The functions check_validity_1 and check_validity_2 take nnode and step_node as inputs. They check if the step node that has been generated is valid or not. It will be invalid if the step node either lies on a black pixel (that is, an obstacle) or if the straight line path joining nnode and step node goes through an obstacle. 0 is returned in case step node is invalid and 1 is returned in case step node is valid.
The function draw_path draws the final path starting from the end_node to the start_node in green color.
void draw_path()
{
Node up, down;
int breaking = 0;
down = end_node;
up = *(end_node.parent);
while(1)
{
line(img, Point(up.position.y, up.position.x), Point(down.position.y, down.position.x), Scalar(0, 255, 0), 2, 8);
if(up.parent == NULL)
break;
up = *(up.parent);
down = *(down.parent);
}
}The rrt() function executes the entire process of generating the random nodes and making the tree.
Generation of a random point:
(rnode->position).x = rand() % 400 + 1;
(rnode->position).y = rand() % 400 + 1;Index indicates the nearest node for a randomly generated node. index = near_node(*rnode);
Calling the stepping function to obtain the step node:
if((node_dist(rnode->position, nodes[index]->position)) < step_size)
return;
else
stepnode->position = stepping(nodes[index]->position, rnode->position);Checking the validity of the step node. If valid, then both flag1 and flag2 would equal 1.
flag1 = check_validity_1(nodes[index]->position, stepnode->position);
flag2 = check_validity_2(nodes[index]->position, stepnode->position);If the stepnode is valid, then stepnode is added to the tree:
nodes[totnodes++] = stepnode;
stepnode->parent = nodes[index];
(nodes[index]->children).push_back(stepnode);Joining the stepnode to the tree by a yellow line:
line(img, Point((stepnode->position).y, (stepnode->position).x), Point(nodes[index]->position.y, nodes[index]->position.x), Scalar(0, 255, 255), 2, 8);Marking the stepnodes green:
for(int i=stepnode->position.x - 2; i < stepnode->position.x + 2; i++)
{
for(int j=stepnode->position.y - 2; j < stepnode->position.y + 2; j++)
{
if((i<0) || (i>400) || (j<0) || (j>400))
continue;
img.at<Vec3b>(i, j)[0] = 0;
img.at<Vec3b>(i, j)[1] = 255;
img.at<Vec3b>(i, j)[2] = 0;
}
}The end_node is added to the tree if it fits the validity criteria and the distance between the end_node and the last step node is less than the step_size.
if((check_validity_1(stepnode->position, end_node.position)) && (check_validity_2(stepnode->position, end_node.position)) && (node_dist(stepnode->position,end_node.position) < step_size))
{
reached = 1;
nodes[totnodes++] = &end_node;
end_node.parent = stepnode;
(nodes[totnodes-1]->children).push_back(&end_node);
}Final path is drawn in green: draw_path(); Iteration number is incremented: iter++; Here is the output image after the implementation of the code:
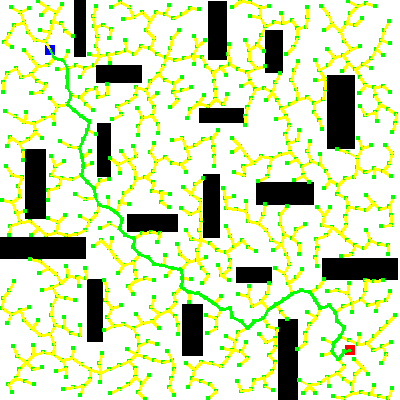
For the complete code, click here. Find another implementation of the RRT Path Planning algorithm here.